まえがき
こんにちは。picturesque(ピクチャレスク)です。
以前に、トートバッグの型紙を作る際の寸法の中で、縫い代をどう含めていくのかを解説した、【137】と【138】の記事がございます。
このたびの【769】はその2記事とも大いに関連し、重複する部分もありますが、この理解こそが今後胸を張ってトートバッグを製作して行けることにつながると考え、まとめのような形で再アップをさせていただいたものです。
マチ付きトートバッグを今後作っていきたい、それを販売もしていきたいなどの前進を目指されるのであれば、是非この時点で根本的な構造のカラクリを知っておかれることをお勧めしたいと思います。
ただ、「こういうものだ」と公式に当てはめるよりも、はるかに「哲学的」なバッグを作ることへの発展の基盤となると思います(^-^)。
型紙を作る直前の計算式

慣れてしまえば、暗算をして型紙もすらすらと作れるようになるかと思います。
最初はじっくり時間をかけて理解して、一度は腑に落ちていただきたいと思います。
ということで、マチ付きのトートバッグの型紙寸法の計算の場面を例としてご紹介します。
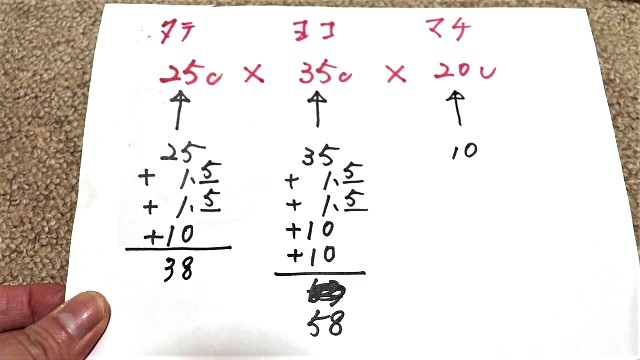
まずとにかく手順から解説を始めてまいります。
縦から行きます。まずはそのまま実寸を置きます。
次に、上下の縫い代を同じ寸法の1.5cmずつ上下の分を足します。
自身の場合、上が大きく縫い代をとるようなことはしておりませんので、上下が同じです。
そして、最後に、マチの出来上がりの半分だけを加えます。
半分であることの理由は、バッグの構造が前面と後ろ面の2つのパーツを合体させるものなので、型紙としては半分になるのです。
これを間違えてマチそのままの寸法にしてしまった経験がありましたが、出来上がりが40cmというおそろしく大きなマチが出来上がってしまいますので間違いですからね。
次に横です。
横も同じように、出来上がりの35cmをまず置きます。
そして、次に、両サイドに縫い代が必要なので、1.5cmを2度足します。
最後にマチですが、横の場合は縦と違ってマチが両サイドに存在しますので、2度足す必要があります。
ただ、あくまでも、半分の構造の分だけなので、2度足すとはいっても、半分の10cmずつを2度足すというものです。
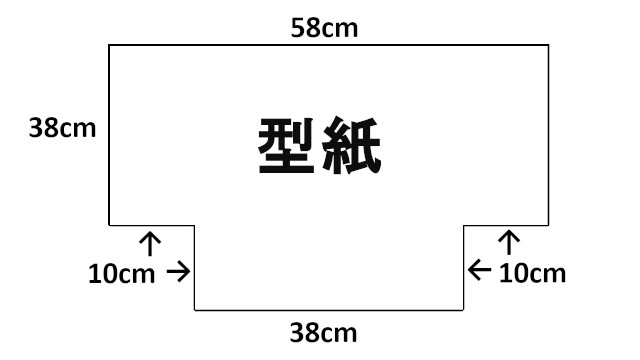
そして、底の左右のマチを型紙から切り抜きます。
マチは、長方形で描いた縦横の値の、38cmx58cmの型紙の端っこの下側をこちらも、半分である10cmで正方形にくり抜きます。
マチには、なぜ縫い代を含めていないのが正解なのかの証明
ここで疑問が1つあるのではないでしょうか。
マチには縫い代を足さなくてよいの?ということです。
こう思ってしまう理由は、マチが立体的に出来上がる構造の物理的な不思議が1つあるからなんです。
実際の製作の場面でマチをつまむと、ぺこんとマチが台形のような形に変わります。
実際にステッチをかけるのは、その台形のトップではなくて、縫い代1.5cmの内陸部です、
そうすると、台形は、底辺が横に余分に突き出していますよね。
この突き出しの分量が、縫い代の1.5cmに等しいのです。
この「等しい」という事実は、過去の【138】の記事で検証記録を綴らせていただきました。
これは物理的な法則とでもいう現象なのか、縫い代が1cmの場合であれば、1cm突き出します。
この台形は、「等脚台形:とうきゃくだいけい」と呼ばれる台形のようで、もしかして物理的な関係があるかもしれなく一応このワードを載せておきます。
また、実際にマチを折る時に真垂直に折っているところも物理的なヒントだと思いますが、自身はまだその見方からは解説出来ておりません。
ただ、あくまで自身の実験でマジックで紙に書いてやってみたことですので、この先もっと「なぜ縫い代の分が垂直に折ると横に高さの1.5cm分ちょうどがはみ出すのか」の論理が深く分かれば追記したいと思います<m(__)m>。
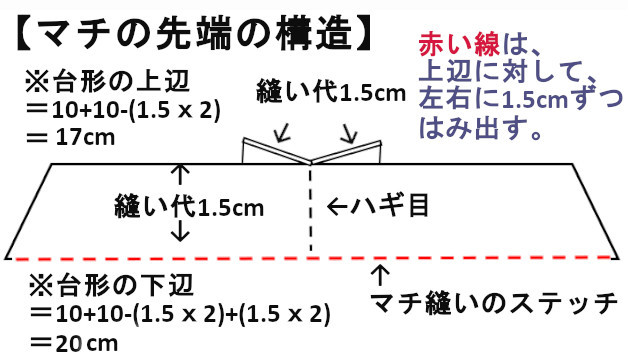
つまり、実寸で計算しておけば、自然に縫い代が含まれているということも言えますし、そもそもマチ部分は、縫い代とは無関係な内側に出来上がるものであるから、すでに、縦横で含めてある縫い代で事足りるということなのです。
この台形の上辺は、型紙の10cmから見ると、継ぎ目の縫い代で1.5cmずつ前面後面のパーツともにとられ、短くなり、10-1.5=8.5cmずつの2パーツで合計17cmしかありません。
しかしです、縫う部分というのは実際は、その1.5cm縫い代をとった下辺(上図では赤い点線)。
そこは、物理的な構造上、縫い代を1.5cm足した長い辺の長さになっているではありませんか。
それが上の17cmに突き出した1.5cmずつを両面分の3cmを足した20cmであるということが事の解明です。
この垂直に折って形作るマチの場合、台形の底辺は縦の長さ1.5cm分上の辺より長くなるようなのです。
どうしても、頭で想像すると、台形の上辺を想像してしまうのですが、実際に縫う場所=実際のマチの出来上がりがその1.5cm下の辺であることがなかなか想像しにくいのです。
この図解で想像だけのイメージと実際の構造が随分違ったものであることに自身も驚いたものです。
ただ、この解説でもまだまだ不足だと思っております。
もっとうまくご説明できるよう今後も考えていきます。
あとがき
このマチの件は奥が深過ぎたかもしれません。
大変多くの人が悩んでおられるようで、腑に落ちていないのだと思います。
どうか、この記事が少しでもヒントになればと思います。
多くの方が腑に落ちない点は、このマチの寸法のカラクリだと思います。
ご協力できる可能な限りを尽くしたいと思います(^-^)。

