まえがき
こんにちは。picturesque(ピクチャレスク)です。
ある日、ハンドメイドバッグノウハウにおける、自らが発信するマチの計算の確認をしていました。
発信するにも見解が偏り過ぎていないかを、時々ネットで確認することがあります。
そうした中、「元の必要寸法が分からない」「割り出し方教えて」の声が溢れんばかりであることに驚愕。
マチ付きというのは3次元の世界観、なかなか想像し辛い混乱があるのだと考えます。
このたびは、「マチ付きトートバッグ」のマチを含めた縫い代込みの寸法の計算方法をお伝えしたいと思います。
つまりは、「出来上がり寸法から逆残によって型紙を作る方法」に等しくなります。
当投稿の【137】では、あれこれとやかく言わずに、とにかく正確な「計算式」を具体例と共にお伝えする回と致します。
出来上がり寸法から型紙を正しく作っていくための「計算式」を中心に、「これを信じて良いのだ」ということを根底にデジタル式にお伝えすることを先にやっていきたいと思います。
「なぜそうなるのか?」という疑問は、【138】【769】【807】【915】で後回し、今すぐ製作していく際には、とりあえず方法論のみの当【137】で十分です。
<マチ>多くのQ&Aでネット上に溢れるマチ付きトートバッグの型紙の作り方(縫い代1.5cmを含んだ型紙)

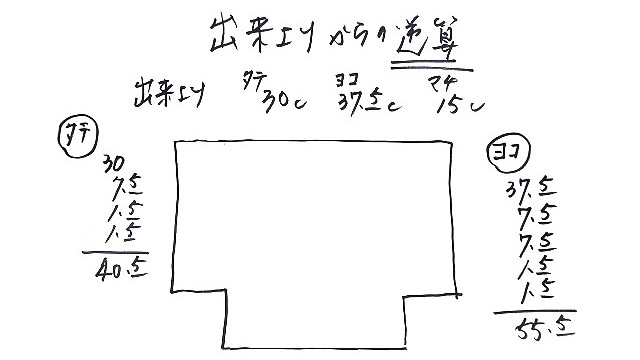
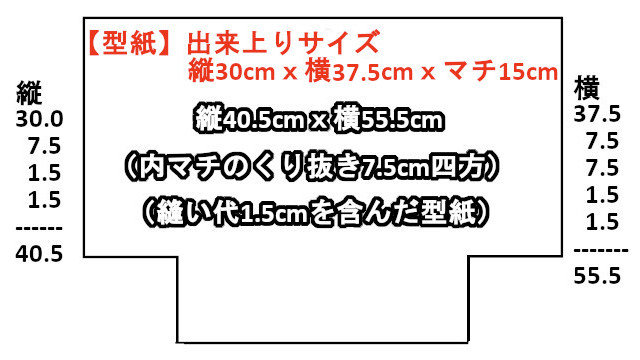
<縦の型紙寸法の算出>
出来上がり寸法に順に積み算していく方法です。
出来上がり寸法30.0cmにマチが必要ですので、片面ずつの合体構造のトートバッグでは半分のマチ寸法ずつと解釈。
30.0cm+7.5cmがまず積み算に配置されます。
残りは、縫い代1.5cmの上下分として2回足すので、図の左側の通り30.0+7.5+1.5+1.5=40.5が縦の長さ。
ピクチャレスクの作り方では上下とも縫い代が同じ1.5cmでやっています。
マチのくり抜きは横の長さが決まってからですので、次は横の型紙へ続きます↓。
<横の型紙寸法の算出>
出来上がり寸法37.5cmにマチが今度は左右共に必要ですので、縦の時と同じように半分ずつの寸法を2回足していきます。
37.5cm+7.5cm+7.5cmがまず積み算に配置されます。
残りは縫い代1.5cmの左右分として2回足すので、図の右側の通り37.5+7.5+7.5+1.5+1.5=55.5cmが横の長さ。
さて、ここで縦40.5cmx横55.5cmの長方形の型紙が出来ましたので、底の左右両方を7.5cm四方の正方形でくり抜き(ハサミでカット)型紙が完成です。
数字が変わっても同じように計算式に当てはめるだけです↓。
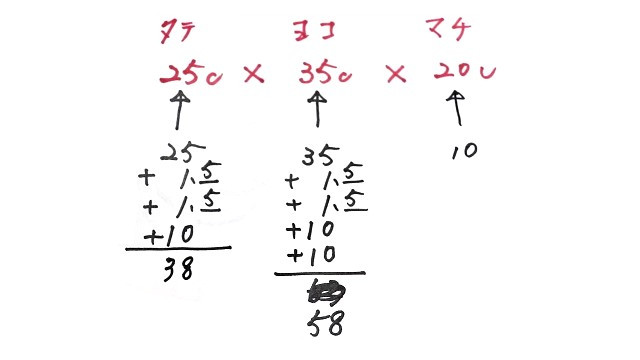
あとがき

このたびは、とにかく方法論のみをお伝えしましたが、もしかして鋭い方は「あれ?」と思われたのではないでしょうか。
図を見るとマチには確かに縫い代が存在するのに、計算の中にマチ用の縫い代が入っていないのでは。。と。

ここで少しだけお伝えしておきますと、実は足して引いているという打ち消し合いにより0(ゼロ)だから加えないということなのです。
そのことも後の【138】【769】【807】【915】において、ご説明していきます。
ただ、先に「こういうものなのだ」というところから入った方が実践的であると判断してこの順番にさせていただいたのでした。
是非素敵なトートバッグを完成されますよう、同じようにハンドメイドバッグを作るピクチャレスクは応援したいと思います(^-^)。

