まえがき
こんにちは。picturesque(ピクチャレスク)です。
当ブログ記事は、2020.07.02に投稿の1つ前の【137】と関連、以前はこちら【138】と1記事に合算してまとめておりました。
それもブログ記事の整頓の1つではあったのですが、その後の更なる「手直し」により、当記事の番がやってきた2025.05.20現在、新規投稿により【137】とは分けることにしたのです。
【137】では、「マチ付きトートバッグの出来上がり寸法からの逆算で作る正しい型紙」の作り方を解説しました。
積み算式に、縦と横を出来上がり寸法からのスタートで正しくマチ寸法と縫い代寸法を加えていく「方法論」のみです。
こうした計算式のみの提示で、数字を当てはめるやり方ですぐに引用できることを優先し、「理由」の部分を後回しにしていたのでした。
この【138】から続く後の【769】【807】【915】は、同様にタイトルに<マチ>が付き、その計算方法の正しさの解明の部分に焦点を当てた投稿なのです。
完全解明には、物理的なところまで迫る難しさがあり、そのことが混乱と複雑さを生むことで、最も基本的なやり方のみの投稿を【137】とさせていただいたのでした。
ということで、このたびからの<マチ>の投稿は、「マチの縫い代を計算式に含めない不思議」を紐解く物理的構造に迫る内容となっていきます。
単純で誰もが同じように実験出来て納得できるようにと、型紙を立体的にして実際にマチを作りミシンで縫う部分に赤マジックを印しました。
型紙を広げた時にその線はどこを走っているのでしょうか。。それがマチの計算式を納得する1つの解明方法になると思います。
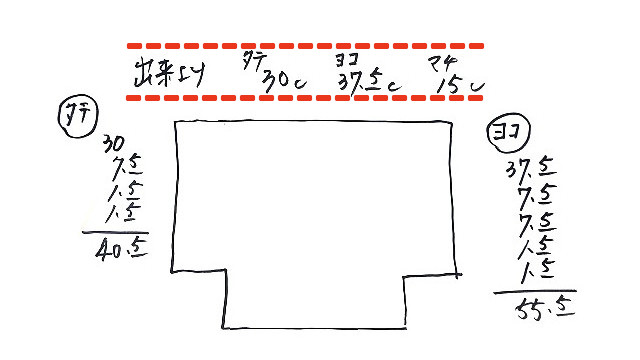
<マチ>マチ付きトートバッグの型紙を立体的に組み立て、縫い代1.5cmに赤線を引いて広げたら出た答え

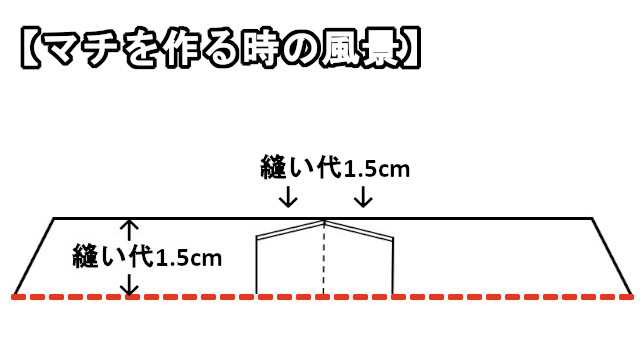



ここで、暗いトンネルを抜け出たかのように明らかになったことは、ミシンで縫っている線は、平面で「Lの字」を縫っていることにイコールであるということ。
言い方を変えますと、実線の方は上糸、点線の方は下糸という見方もできます。
どうでしょう、マジックの線が型紙の1.5cm内側を完全に覆ったという実証から、逆説的に「マチに縫い代1.5cmを含めていないのに正しく出来上がった」と言える実験結果です。

左側は、本体の底の縫い代1.5cmに該当しますので、マチからは削除の9-1.5=7.5cmがマチの領域。
出来上がりのマチ7.5cm分よりも1.5cm右にはみ出して奪った1.5cm分は、底の縫い代である左側1.5cmと重複することの余分と打ち消し合って「0:ゼロ」なのだという見方で腑に落ちませんか?。
このたびは、ここまでです。
あとがき
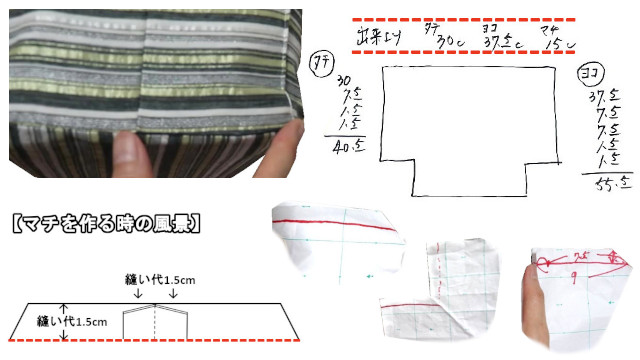
このたびの赤マジックの検証でも、随分クリアになってきたのではないでしょうか。
私は、この実験をするまでこのような構造すらイメージできていませんでした。
しかし、今後アウトプットして多くの方にお伝えしていくにはもっと深堀りして腑に落ちねばとやってみたことでした。
じゃあ、縫い代が底は1.5cmでもマチの方が1cmという風に同じ縫い代ではない場合はどうなるのか。。など、多様なケースでやってみて、物理的法則や構造を掴んでいくことになります。
というわけで、続く【769】【807】【915】も投稿があるのです。
自らが納得したお品物は、きっと優れたお品物になっていくと思うのです。
素敵なバッグが完成できますよう、応援したいと思います(^-^)。

